Cosmological Phase Transitions
It is widely believed that phase transitions have occurred; the Standard Model of particle physics predicts at least two of these transitions (the electroweak phase transition and the quantum chromo-dynamics phase transition) whose cosmological signature has not yet been detected. It is also likely that the Standard Model is an effective field theory (Georgi:1994qn), and phase transitions have occurred in sectors not yet understood. These transitions most likely occurred at a range of different scales: during inflation, ending inflation, and many scales since (from the GUT scale down to the electroweak scale).
Recent experimental advances in understanding electroweak physics and the parameters associated with the Higgs boson (ATLAS:2012ae, Chatrchyan:2012tx) are just a part of the continuing importance of understanding the electroweak phase transition. We are gaining a better understanding of the mass, couplings and structure of the Higgs and its relation to other standard model particles; we can write down the models of the Higgs potential and begin to make precision predictions about the cosmological implications of the electroweak phase transition.
Gravitational Radiation from Phase transitions.
The estimates of the gravitational radiation from cosmological processes date to the the early 1980's (Witten:1984rs); however, the first serious attempts at estimating the power radiated from the collisions of bubbles during first-order phase transitions came somewhat later (Kosowsky:1991ua, Turner:1992tz, Kosowsky:1992rz, Kosowsky:1992vn). These estimates were based on both analytic arguments and numerical simulations involving a small number of bubbles. We took a more direct path. Since the initial conditions for the bubbles are known (Coleman:1977py, Coleman:1980aw), we set up a network of bubbles on a lattice. These bubbles are then able to expand and interact via the equations of motion of the fields. The field configuration then sources the gravitational radiation and we are able to calculate the lingering power spectrum. The image below shows three time slices for such of a sample simulation and the final gravitational wave amplitude.
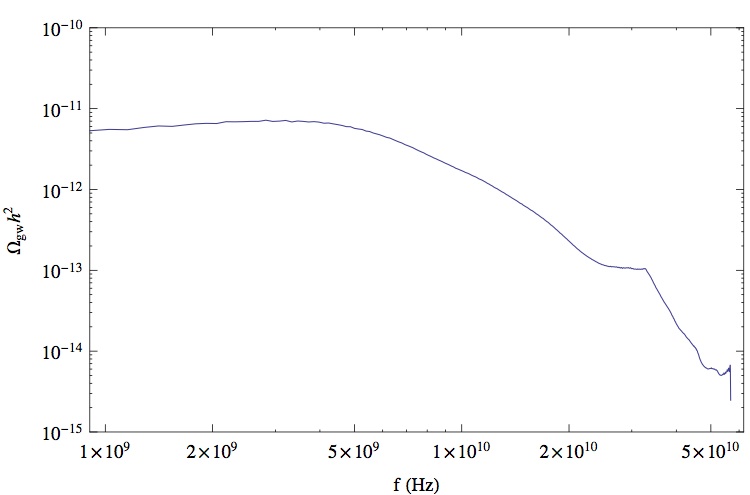
These simulations are groundbreaking and represent a huge success in the modeling of phase transitions. The success of these simulations have put our eye to more realistic models to address: (1) this gravitational radiation is outside of the detectable limit in the near future and (2) mediating phase transitions only with scalar fields misses some of the physics associated with the transition. We discuss how we plan to extend this work.
Dynamical symmetry breaking, introduced by (Krauss:1991qu, JonesSmith:2007ne, Krauss:2010df) or alternatively described by (Fenu:2009qf), can source gravitational radiation after a second order phase transition. In this case, the phase transition itself is smooth, and one does not expect the rapid burst of gravitational radiation. Xavier Siemens (University of Wisconsin, Milwaukee), Larry Price (CalTech), Brian Vleck (University of Wisconsin, Milwaukee) and I used the lattice to study this type of phase transition as well. Here we begin with an N-dimensional classical field. At high energies the associated potential is O(N) symmetric and massive. As the Universe cools, the potential obtains a minimum with an O(N-1) symmetric vacuum state.
Since this transition is occurring dynamically, the field in each Hubble-sized patch of the Universe achieves some (different) expectation value as it settles into the degenerate minimum. As the Universe expands in a radiation dominated era, the Hubble horizon expands and these regions interact. Because the value of the field in each region is independent, there now exist gradient terms in the field; these gradient terms generate anisotropic stress which sources gravitational radiation as the fields realign. Since the horizon is changing during the transition radiation is generated over a wide range of wavelengths. This leads to a scale invariant power spectrum of gravitational waves that might mimic the spectrum generically produced during inflation. This gravitational wave background from such transitions has been estimated by the authors of the model, but they have never been (accurately calculated) until now. We verify that the gravitational wave spectrum from the reordering of the fields after the transition is indeed scale-invariant, and parameterize the resulting power spectrum. Complete results can be found in (Giblin:2011yh).
The next great step in our quest toward understanding these phase transitions is to include the effects of all the coupled degrees of freedom. We are in the process of incorporating relativisitic fluids into these models, so come back for updates as we complete this part of the project.